Algoritam
U matematici i informatici, algoritam je konačni niz precizno definiranih, računalno izvedljivih uputa, tipično za rješavanje klase problema ili za izvršavanje računa. Algoritmi su uvijek nedvosmisleni i koriste se kao specifikacije za obavljanje izračuna, obrade podataka, automatiziranog zaključivanja i drugih zadataka.
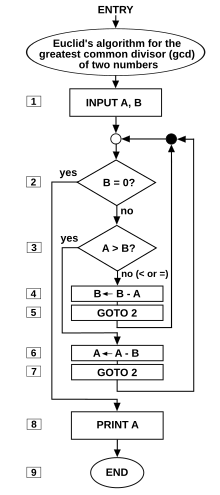

Kao učinkovita metoda, algoritam se može izraziti unutar ograničene količine prostora i vremena, i u dobro definiranom formalnom jeziku za izračunavanje funkcije. Polazeći od početnog stanja i inicijalnog unosa (možda i praznog), upute opisuju izračun koji se, kada se izvodi, nastavlja kroz ograničeni broj dobro definiranih sukcesivnih stanja, na kraju stvarajući "izlaz" i završava u konačnom završnom stanju. Prijelaz iz jednog stanja u drugo nije nužno determinističko; neki algoritmi, poznati kao randomizirani algoritmi, uključuju nasumični unos.
Koncept algoritma postoji još od antike. Aritmetičke algoritme, kao što je algoritam za podjelu, koristili su stari babilonski matematičari c. 2500. godine prije Krista i egipatski matematičari c. 1550. pr. Grčki su matematičari kasnije koristili algoritme na sito Eratostena za pronalazak pravih brojeva, i euklidski algoritam za pronalaženje najvećeg zajedničkog djelitelja dva broja. Arapski matematičari kao što je Al-Kindi u 9. stoljeću koristili su kriptografske algoritme za probijanje koda temeljeni na frekvencijskoj analizi.
Sama riječ algoritam potječe od perzijskog matematičara iz 9. stoljeća Muḥammada ibn Mūsā Mūsā al-Khwārizmī, latiniziranoAlgoritmija. Djelomična formalizacija onoga što bi postalo moderni koncept algoritma započela je pokušajima da se riješi Entscheidungsproblem (problem odluke) koji je postavio David Hilbert 1928. godine. Kasnije su formalizacije definirane kao pokušaji definiranja "učinkovite proračunljivosti " ili "učinkovite metode". Te formalizacije obuhvaćale su rekurzivne funkcije Gödel - Herbrand - Kleene iz 1930., 1934. i 1935., lambda računica Crkve Alonza iz 1936., Formulacija 1 Emila Pota iz 1936. i Turingovoga stroja Alana Turinga iz 1936–37 i 1939.
Etimologija
urediRiječ 'algoritam' svoje korijene ima u latinizaciji imena perzijskog matematičara Muhammeda ibn Musa al-Khwarizmija u prvim koracima prema algorizmu. Al-Khwarizmi (Arapski: الخوارزمي, Perzijski: خوارزمی, c. 780–850) bio je perzijski matematičar, astronom, geograf i znanstvenik u Kući mudrosti u Bagdadu, čije ime znači „porijeklom iz Hvarazma “, regije koja je bila dio Velikog Irana, a sada je u Uzbekistanu.
Na engleskom jeziku izraz algoritam prvi puta je korišten 1230., a zatim ga je spomenuo Chaucer 1391. godine. Engleski je usvojio francuski izraz, ali tek je u 19. stoljeću "algoritam" poprimio značenje koje ima u modernom engleskom.
Još jedna rana upotreba riječi je iz 1240., u priručniku pod nazivom Carmen de Algorismo koji je napisao Alexandre de Villedieu. Započinje s:
što u prijevodu znači:
Pjesma je dugačka nekoliko stotina redaka i sažima umjetnost izračuna s novim stilom indijskih kockica, ili Talibus Indorum, ili hinduističkim brojevima.
Oblikovanje algoritma
urediTipični koraci u razvoju algoritama:
- Definicija problema
- Razvoj modela
- Specifikacija algoritma
- Izrada algoritma
- Provjera ispravnosti algoritma
- Analiza algoritma
- Provedba algoritma
- Testiranje programa
- Priprema dokumentacije
Implementacija
urediVećina algoritama predviđena je za implementaciju u obliku računalnih programa. Međutim, algoritmi se također primjenjuju na druge načine, na primjer, u biološkoj neurološkoj mreži (na primjer, ljudski mozak koji provodi aritmetiku ili insekt koji traži hranu), u električnom krugu ili u mehaničkom uređaju.
Računalni algoritmi
urediU računalnim sustavima algoritam je u primjer logike koju je u softveru napisao proizvođač softvera, kako bi bio učinkovit za namjeravano "ciljno" računalo (računala) da proizvedu izlaz s danog (možda nultu) ulaza. Optimalni algoritam, čak i pokretanje starog hardvera, dao bi brže rezultate od ne-optimalnog algoritma (veće složenosti vremena) za istu svrhu, koji radi u učinkovitijem hardveru; zato se algoritmi, poput računalnog hardvera, smatraju tehnologijom.
Primjeri
urediPrimjer algoritma
urediJedan od najjednostavnijih algoritama je pronaći najveći broj na popisu brojeva slučajnim redoslijedom. Pronalaženje rješenja zahtijeva uvid u svaki broj na popisu. Iz ovoga slijedi jednostavan algoritam koji se u opisu na visokoj razini u engleskoj prozi može opisati u sljedećim koracima:
- Ako u skupu nema brojeva, onda nema ni najvišeg broja.
- Pretpostavimo da je prvi broj u setu najveći broj u setu.
- Za svaki preostali broj u skupu: ako je taj broj veći od trenutno najvećeg broja, smatrajte ovaj broj najvećim brojem u skupu.
- Kada u setu ne ostane nijedan broj koji treba ponoviti, smatrajte da je trenutno najveći broj najveći broj skupa.
Unos: A list of numbers L. Ispis: The largest number in the list L.
if L.size = 0 return null
largest ← L[0]
for each item in L, do
if item > largest, then
largest ← item
return largest
Kontinuirani algoritmi
urediDefinicija kontinuiranog algoritma:
- Algoritam koji radi na podacima koji predstavljaju kontinuirane količine, iako su ti podaci predstavljeni diskretnim aproksimacijama - takvi se algoritmi proučavaju u numeričkoj analizi; ili
- Algoritam u obliku diferencijalne jednadžbe koji djeluje kontinuirano na podatke i radi na analognom računalu.