Princip stacionarnog djelovanja

Princip stacionarnog djelovanja jedan je od temeljnih načela fizike. Govori o tome kako će putanja kojom će neki fizikalni sustav poći, biti ona za koju je određena fizikalna veličina, nazvana djelovanje, ekstremizirana. Sustavi će se u prirodi uvijek odvijati na optimalni način, a taj optimalan način je kad je djelovanje ekstremizirano.

Princip stacionarnog djelovanja ekvivalentan je i omogućuje izvođenje diferencijalnih jednadžbi gibanja fizičkog sustava. Iako je izvorno formuliran za klasičnu mehaniku, primjenjuje se na klasična polja kao što su elektromagnetsko i gravitacijsko polje, te igra važnu ulogu u optici, kvantnoj mehanici, kvantnoj teoriji polja, općoj teoriji relativnosti i drugima.

Cijelo razmatranje principa stacionarnog djelovanja započinje potragom za krivuljom najbržeg spusta loptice između dvije točke.

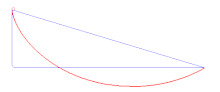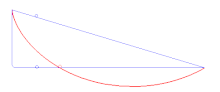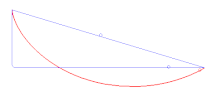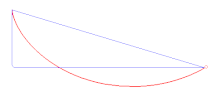
Problem Brachistochrone kojeg je postavio Johann Bernoulli. Krivulja najbržeg spusta je cikloida (crveno), a ne ravna linija (plave).

Povijesno gledano, ideja o pronalaženju najkraćeg puta koji čestica može slijediti ovisno o sili motivirala je prve primjene varijacijskog računa na mehaničke probleme, kao što je problem Brachistochrone (iz antičkog grčkog βράχιστος χρόνος (brákhistos khrónos) 'najkraće vrijeme') kojeg su riješili Johann Bernoulli 1696. (Johann Bernoulli je postavio taj problem u Acta Eruditorum u lipnju, 1696.), kao i Leibniz, Daniel Bernoulli, L'Hôpital otprilike u isto vrijeme, a Newton sljedeće godine.^[1] Sam Newton je razmišljao u skladu s varijacijskim računom, ali to nikad nije objavio. Ovaj problem, odnosno ideje koje su proizišle iz njega vode do varijacijskih principa mehanike, odnosno do principa stacionarnog djelovanja kojeg su razvili Fermat, Maupertuis, Euler, Lagrange, Hamilton i drugi.

Maupertuisov princip

Pierre Louis Maupertuis bio je prvi koji je objavio princip najmanjeg djelovanja, kao način prilagodbe Fermatova principa za valove korpuskularnoj (čestičnoj) teoriji svjetlosti.^[2] Pierre de Fermat je objasnio Snellov zakon za lom svjetlosti pod pretpostavkom da svjetlost prati put najkraćeg vremena, a ne udaljenost. To je mučilo Maupertuisa, budući da je smatrao da bi vrijeme i udaljenost trebali biti izjednačeni: "Zašto bi svjetlost preferirala put najkraćeg vremena u odnosu na put udaljenosti?" Maupertuis je svoj postupak definirao kao varijaciju sljedeće veličine

$S=\sum mvs$

gdje je $S$ djelovanje koje je trebalo biti minimizirao na svim stazama koje povezuju dvije točke. Bio je ismijavan od ostatka prosvjetiteljske elite, poput Voltairea i Koeniga.^[3]

Euler i Lagrange

Jedan od rijetkih koji je uvidio značaj Maupertuisovog principa stacionarnog djelovanja i branio ga bio je švicarski matematičar Leonhard Euler.

Prvo što je Euler napravio, bilo je da je zamijenio sumu za integral i dobio sljedeći izraz

$S=\int mvds$

znajući kako je $v={\frac {ds}{dt}}$ , odnosno $ds=vdt$ i uvrštavajući to u prethodnu formulu dobio je

$S=\int mv^{2}dt=\int 2E_{k}dt$

Odnosno, integral brzine po putu pretvorio je u integral kinetičke energije po vremenu.

Prateći njegove korake, glavnu ulogu preuzeo je mladi talijanski matematičar Joseph-Louis Lagrange koji je unaprijedio izraz i došao do sljedeće verzije

${S}=\int _{t_{1}}^{t_{2}}L\,dt=\int _{t_{1}}^{t_{2}}\left(T-U\right)dt$

Ovo je definicija djelovanja koja je uvriježena i na ovaj način se zapisuje kad se predaje studentima. Djelovanje je funkcionalna jednadžba, integral Lagrangeove funkcije $L$ između dva vremenska trenutka koja izbacuje skalarnu vrijednost i ima mjernu jedinicu $Js$ joule-sekunda.

Princip stacionarnog djelovanja nam kaže kako je prava evolucija $q(t)$ sustava evolucija za koju djelovanje $S$ stacionarno (minimum, ili sedlasta točka). Ovaj princip rezultira jednadžbama gibanja u Lagrangeovoj mehanici.

Hamiltonov princip

Kako sustav evoluira, q prati put u konfiguracijskom prostoru (samo neki putevi su pokazani). Put kojim će sustav poći (crveni) ima stacionarno djelovanje (δS = 0) uslijed malih promjena konfiguraija sustava (δq).^[4]

Najpoznatiju formulaciju principa stacionarnog djelovanja postavio je Irski matematičar William Rowan Hamilton, koji je naravno gradio na rezultatima prijašnjih matematičara i fizičara kao što su Mapertuis, Euler i Lagrange.

Matematička formulacija

Hamiltonov princip kaže da je prava evolucija $q(t)$ sustava opisanog s $n$ poopćenih koordinata ona u kojoj je varijacija djelovanja ${\mathcal {S}}[\mathbf {q} ]\ {\stackrel {\mathrm {def} }{=}}\ \int _{t_{1}}^{t_{2}}L(\mathbf {q} (t),{\dot {\mathbf {q} }}(t),t)\,dt$ gdje je $L(\mathbf {q} ,{\dot {\mathbf {q} }},t)$ Lagrangeova funkcija, jednaka nuli.

Odnosno

$\delta S=0$

Drugim riječima, svaka perturbacija prvog reda prave evolucije sustava rezultira (najviše) promjenama drugog reda u ${\mathcal {S}}$ .

Iz ovog principa mogu se izvesti sve diferencijalne jednadžbe gibanja klasične mehanike. Euler-Lagrangeova jednadžba ekvivalentna je i slijedi iz Hamiltonovog principa stacionarnog djelovanja.

Neka je $q(t)$ prava evolucija sustava između dva stanja $q_{1}=q(t_{1})$ i $q_{2}=q(t_{2})$ u dva trenutka $t_{1}$ i $t_{2}$ , i neka je $\epsilon$ mala perturbacija sustava koje je nula na krajevima putanje ${\boldsymbol {\varepsilon }}(t_{1})={\boldsymbol {\varepsilon }}(t_{2})\ {\stackrel {\mathrm {def} }{=}}\ 0$

Perturbacija funkcionala djelovanja $\delta {\mathcal {S}}$ bila bi $\delta {\mathcal {S}}=\int _{t_{1}}^{t_{2}}\;\left[L(\mathbf {q} +{\boldsymbol {\varepsilon }},{\dot {\mathbf {q} }}+{\dot {\boldsymbol {\varepsilon }}})-L(\mathbf {q} ,{\dot {\mathbf {q} }})\right]dt=\int _{t_{1}}^{t_{2}}\;\left({\boldsymbol {\varepsilon }}\cdot {\frac {\partial L}{\partial \mathbf {q} }}+{\dot {\boldsymbol {\varepsilon }}}\cdot {\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}\right)\,dt$

Ukoliko napravimo parcijalnu integraciju $\delta {\mathcal {S}}=\left[{\boldsymbol {\varepsilon }}\cdot {\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}\right]_{t_{1}}^{t_{2}}+\int _{t_{1}}^{t_{2}}\;\left({\boldsymbol {\varepsilon }}\cdot {\frac {\partial L}{\partial \mathbf {q} }}-{\boldsymbol {\varepsilon }}\cdot {\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}\right)\,dt$

Rubni uvjeti ${\boldsymbol {\varepsilon }}(t_{1})={\boldsymbol {\varepsilon }}(t_{2})\ {\stackrel {\mathrm {def} }{=}}\ 0$ uklanjaju prvi član

$\delta {\mathcal {S}}=\int _{t_{1}}^{t_{2}}\;{\boldsymbol {\varepsilon }}\cdot \left({\frac {\partial L}{\partial \mathbf {q} }}-{\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}\right)\,dt=0$

Hamiltonov princip kaže kako je perturbacija prvog reda $\delta {\mathcal {S}}$ nula za sve moguće perturbacije $\epsilon$ . Pošto $\epsilon$ može poprimiti bilo koju vrijednost, jednadžba će biti ekstemizirana (varijacija jednaka nuli) jedino kad je

${\frac {\partial L}{\partial \mathbf {q} }}-{\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}=0$

Ovo je takozvana Euler-Lagrangeova jednadžba analitičke mehanike.

Izvori

↑ Hand, L. N.; Finch, J. D. (1998). Analytical Mechanics (2nd ed.). Cambridge University Press. ISBN 9780521575720.
↑ Whittaker, Edmund T. (1989). A history of the theories of aether & electricity. 2: The modern theories, 1900 - 1926 (Repr ed.). New York: Dover Publ. ISBN 978-0-486-26126-3.
↑ Fee, Jerome (1942). "Maupertuis and the Principle of Least Action". American Scientist. 30 (2): 149–158. ISSN 0003-0996. JSTOR 27825934.
↑ R. Penrose. 2007. The Road to Reality. Vintage books. str. 474. ISBN 978-0-679-77631-4

[1] Hand, L. N.; Finch, J. D. (1998). Analytical Mechanics (2nd ed.). Cambridge University Press. ISBN 9780521575720.

[2] Whittaker, Edmund T. (1989). A history of the theories of aether & electricity. 2: The modern theories, 1900 - 1926 (Repr ed.). New York: Dover Publ. ISBN 978-0-486-26126-3.

[3] Fee, Jerome (1942). "Maupertuis and the Principle of Least Action". American Scientist. 30 (2): 149–158. ISSN 0003-0996. JSTOR 27825934.

[penrose-4] R. Penrose. 2007. The Road to Reality. Vintage books. str. 474. ISBN 978-0-679-77631-4

[1]

[2]

[3]

[4]